Двоична бройна система

[mohaha]

В двоичната бройна система се използват само цифрите 1 и 0. Взети поотделно те изразяват едно и нула, но написани заедно могат да изразят бройчно число. Например 1101 ( чете се едно едно нула едно ) отговаря на числото 13, а 11011101 отговаря на десетичното число 221. В двоичната бройна система 0 може да се напише като 00 или 000 и т.н. Също така двоичното число 1101 може да се напише 01101 или 001101 и т.н. Тоест от ляво може да се прибавят нули, но това не променя числото. В техниката изразът "двоична цифра" често се заменя с термина бит. По такъв начин двоичното число 1101 е четирибитово, а 10001001 ( 137 ) е осембитово.
Двоичната бройна система е също позиционна, като "стойността" на всяка следваща позиция ( от дясно на ляво ) е 2 пъти по-голяма от тази на предишната.
Пример:
За да разберем двоичното число 010101 на кое десетично число е равно пресмятаме така:
0   1   0    1   0    1
|   |    |    |    |    |
|   |    |    |    |    |__1х1=1
|   |    |    |    |_____0х2=0
|   |    |    |________1х4=4
|   |    |___________0х8=0
|   |______________1х16=16
|________________0х32=0

Сумираме разултатите и получаваме 21 => 010101=21
Използвал съм матерял от книгата "Аз овладявам копютъра" на Доц. д-р инж. Атанас Шишков, но с промени ( защото ако го бях писал сам половината форум нямаше да ме разбере  :lol: ).
Ако някой открие грешки да казва бързо .
ПП. Размества се при графиката. :?
ПП.2 Явно може да се оставя само по един интервал... Дано ме разберете. Аз все пак ще направя картинка.

[Gnus]

Екстра е. Само дето 10001001 е 137,  а не 73.

[mohaha]

Даааа... Извинявам се за грешката незнам защо съм го писал така  :oops:  :lol: . Ама то 73 и 137 са си близо  :lol: .
ПП. Оправих го. Благодаря за забележката!  

[Gnus]

Ами те са си близки. 73 = 1001001

ПП. Опа, така е, който не чете до край. Сега видях, че и ти това си написал

[zbytsam]

Мисля че има и малко по лесен вариант :

Примерно взимаме числото 01011101. Разглеждаме числото от дясно на ляво
и в този ред го степенуваме, като най-дясното ни е на нулева степен ,следващоото на степен1ва, по-следващото на степен втора и така до първото от ляво , което ни е на степен 7ма,защото числото има 8 цифри.

Важно е да помним , че всяко число на степен 0 е равно на 1.

Така например тва число ни се получава 93

01011101 = 0*2^7 + 1*2^6 + 0*2^5 + 1*2^4 + 1*2^3+ 1*2^2 + 0*2+1.2^0=93

[kristiman]

да и аз това исках да кажа


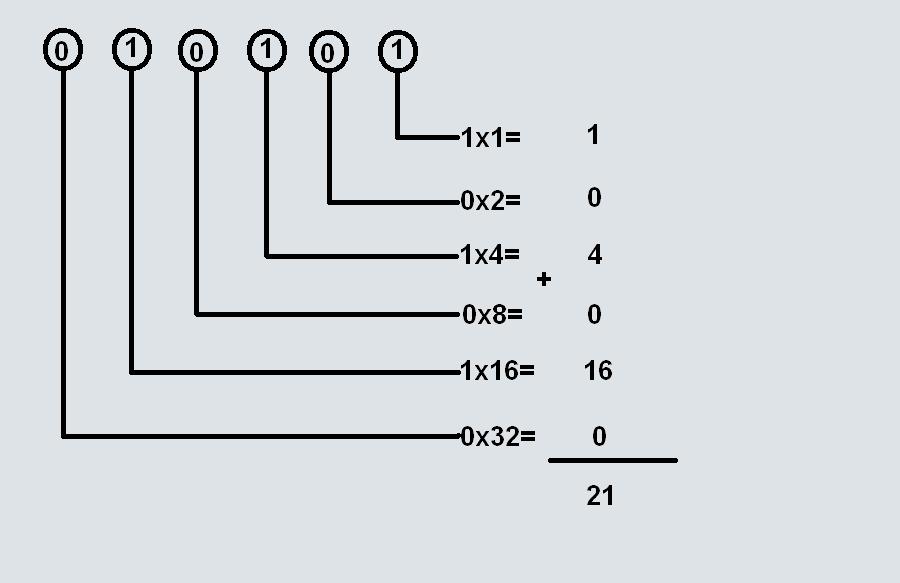
числото "abcdef" в двуична бройна система е равно на :
f*(1*2^0) + e*(1*2^1) + d*(1*2^2) + c*(1*2^3) + b*(1*2^4) + a*(1*2^5) = f*1+e*2+d*4+c*8+b*16+a*32

гледам че не си обяснил как става от десетична в двуична

за да превърнем числото 1123,което е в десетична бройна система,в двуична бройна система го делим на 2 и пишем резултата в ляво на вече искараните цифри

значи делим 1123 на 2 и получаваме 561 със остатък 1 ( или както се пише в 4-ти клас -> 561 (1)   )
така записваме в крайната стойност 1

делим 561 на 2 и получаваме 280 (1)
записваме и тази единица в крайното число ,и то става -> 11

делим 280 на 2 и получаваме 140 (0) (това че остатъка е "0" не е нужно да се пише,но е важно за да не се объркате)
записваме тази нула и крайното число става -> 011

нататък ще смятам без думи

140:2=70 (0) -> 0011

70:2=35 (0) -> 00011

35:2=17(1) -> 100011

17:2=8(1) -> 1100011

8:2=4(0) -> 01100011

4:2=2(0) -> 001100011

2:2=1(0) -> 0001100011

и е МНОГО важно като стигнем до резултат "1" да не забравяме че и "1" се дели !
=> 1:2=0(1) -> 10001100011

препоръчително е да смятате до тук,защото 0:2 винаги ще е равно на 0   .Разбира се,ако продължите да смятате не е проблем,защото става следното:

0:2=0(0) -> 010001100011
0:2=0(0) -> 0010001100011
0:2=0(0) -> 00010001100011
и т.н. ,но както разбрахме от mohaha,като прибавяме "0" в лявата част на едно число (независимо от бройната система в която е [пример: 0199=199 ; 1000110 = 000001000110]) то си остава същото

моля кажете ако съм сгрешил някъде че да не се обърка някой


П.П. между другото zbytsam го обясни добре ,но все пак с букви смятам,че по се разбира,защото числата са доста
mohaha качи си тази снимчица: